Topic

An overview of how to sort a collection of elements that may be split over several arrays.

Motivation

There are certain situations where it is necessary to sort a collection of logical elements that might span two or more separate arrays. This comes up a lot in situations where we might be using a structure of arrays (SOA) approach (popular among the data orientated design (DOD) crowd). This article offers one possible solution inspired by an incredible series on The Old New Thing blog by Raymond Chen.

Example

Suppose we have a type called thing_t which contains an id, transform, rigid body and collider.

struct thing_t
{
    int64_t id;
    mat4_t transform;
    rigid_body_t rigid_body;
    collider_t collider;
};

thing_t things[100];

We keep our thing_t instances in an array as we’ll iterate over them quite a bit. By doing this we take advantage of the cache locality provided by arrays (each element being contiguous in memory).

We also want to be able to perform fast look-ups into the array so we keep the thing_t instances sorted by their id. This allows us to use std::equal_range to perform a binary search in O(log n) time instead of a linear search taking O(n) time.

This works great for a while, but after some time we realize we’re usually only accessing the transform and not touching the rigid_body_t or collider_t fields anywhere near as often. It’d be great to not be wasting all this memory on each cache line with each read of thing_t, so data orientated design (DOD) to the rescue, we decide to split out the parts of thing_t into individual arrays that we can iterate over separately.

int64_t thing_ids[100];
mat4_t thing_transforms[100];
rigid_body_t thing_rigid_bodies[100];
float thing_colliders[100];

This sits behind an interface so we can request a transform using const mat4_t& ThingTransform(int32_t index) instead of accessing the transform on the thing_t instance with something like const thing_t& GetThing(int32_t index) and thing.transform. The problem comes when we realize we need to sort each separate array by the id.

Previously we’d been using std::sort and everything worked as expected.

std::sort(std::begin(things), std::end(things),
  [](const auto& lhs, const auto& rhs) { return lhs.m_id < rhs.m_id; });

Unfortunately having separate arrays throws a bit of a spanner in the works. There isn’t an obvious way to sort the individual arrays by the id. Fortunately there’s an elegant solution that builds on top of applying a permutation to an array/vector.

Note: I’m switching to std::vector from here on but the principal is the same as if we were just using plain old arrays.

// credit Raymond Chen, The Old New Thing blog
// https://devblogs.microsoft.com/oldnewthing/20170102-00/?p=95095
template<typename T>
void
apply_permutation(
  std::vector<T>& v, std::vector<int>& indices)
{
  using std::swap;
  for (size_t i = 0; i < indices.size(); i++) {
    auto current = i;
    while (i != indices[current]) {
      auto next = indices[current];
      swap(v[current], v[next]);
      indices[current] = current;
      current = next;
    }
    indices[current] = current;
  }
}

I’m not going to go through this algorithm in detail here, to understand it fully please go read the excellent post by Raymond Chen here (and all subsequent posts, listed at the bottom of the page).

The incredibly abridged version is we do v[i] = v[indices[i]], (where indices is the sorted array) neatly handling overwriting any elements. Everything in v gets moved into the correct place.

With this handy utility added to our toolbox we can now make use of it while sorting.

// credit Raymond Chen, The Old New Thing blog
// https://devblogs.microsoft.com/oldnewthing/20170105-00/?p=95125
template <typename T, typename Compare>
void sort_minimize_copies(std::vector<T>& v, Compare cmp)
{
  std::vector<int> indices(v.size());
  std::iota(indices.begin(), indices.end(), 0);
  std::sort(indices.begin(), indices.end(), cmp);
  apply_permutation(v, indices);
}

First we create an ordered list of integers (using std::iota, that generates a list of sequentially increasing values), and then sort that list according to the cmp predicate. The sorted integers can then be passed to apply_permutation to update the order of the elements in v.

So to sort our transforms we can write this:

sort_minimize_copies(
  thing_transforms, [&thing_ids](auto lhs, auto rhs) {
    return thing_ids[lhs] < thing_ids[rhs];
  });

This is great, but we still have a problem where we need to call this function multiple times for each separate array we want to sort, which involves a lot of wasted work (we need to sort the thing_ids itself, as well as the rigid bodies and colliders). What would be nice is to be able to pass in all arrays we’d like to be updated according to the sort order. That way the sort only has to happen once, and we update all the arrays in one go.

This last part is a small refinement I made to handle this case.

// inspired by Raymond Chen, The Old New Thing blog
// https://devblogs.microsoft.com/oldnewthing/20170102-00/?p=95095
// updates - Tom Hulton-Harrop
template <typename... Iter>
void apply_permutation_again(
  const int32_t begin, const int32_t end,
  std::vector<int>& indices, Iter... iters)
{
  using std::swap;
  for (int32_t i = begin; i < end; i++) {
    auto current = i;
    while (i != indices[current - begin]) {
      auto next = indices[current - begin];
      ([&](const auto it) {swap(it[current - begin], it[next - begin]);}(
        iters),
      ...);
      indices[current - begin] = current;
      current = next;
    }
    indices[current - begin] = current;
  }
}

template <typename Compare, typename... Iter>
void sort_minimize_copies_again(
const int32_t begin, const int32_t end, Compare&& cmp, Iter... it)
{
  std::vector<int> indices(end-begin);
  std::iota(indices.begin(), indices.end(), 0);
  std::sort(indices.begin(), indices.end(), std::forward<Compare>(cmp));
  apply_permutation_again(begin, end, indices, it...);
}

The first change is instead of passing a std::vector with the type to sort, we pass a begin/end index (offsets) to specify the range to sort. We next pass the vector of indices as before, and after we use a variadic template with a parameter pack to refer to all the arrays to sort. The syntax looks a little confusing but essentially what we’re doing is calling swap on every iterator we pass in using a fold expression (right now the expectation is to always pass begin, there could actually be a cleverer way to write this which takes iterator pairs but this was good enough for this particular use case).

We can now use it like this:

sort_minimize_copies_again(
  0, thing_ids.size(), [&thing_ids](auto lhs, auto rhs) {
    return thing_ids[lhs] < thing_ids[rhs];
  },
  std::begin(thing_ids), std::begin(thing_transforms),
  std::begin(thing_rigid_bodies), std::begin(thing_colliders));

This only performs the sort once, and will move all the elements in each array into the right position.

Note: Do be careful to ensure all std::vectors remain the same size otherwise things will likely go horribly wrong…

Deliberation

To see the performance difference between the different approaches take a look at this quick-bench example. The results vary depending on the compiler and standard library used, but in some cases the sort where we minimize copies and/or moves using the SOA layout is actually faster than the traditional AOS approach.

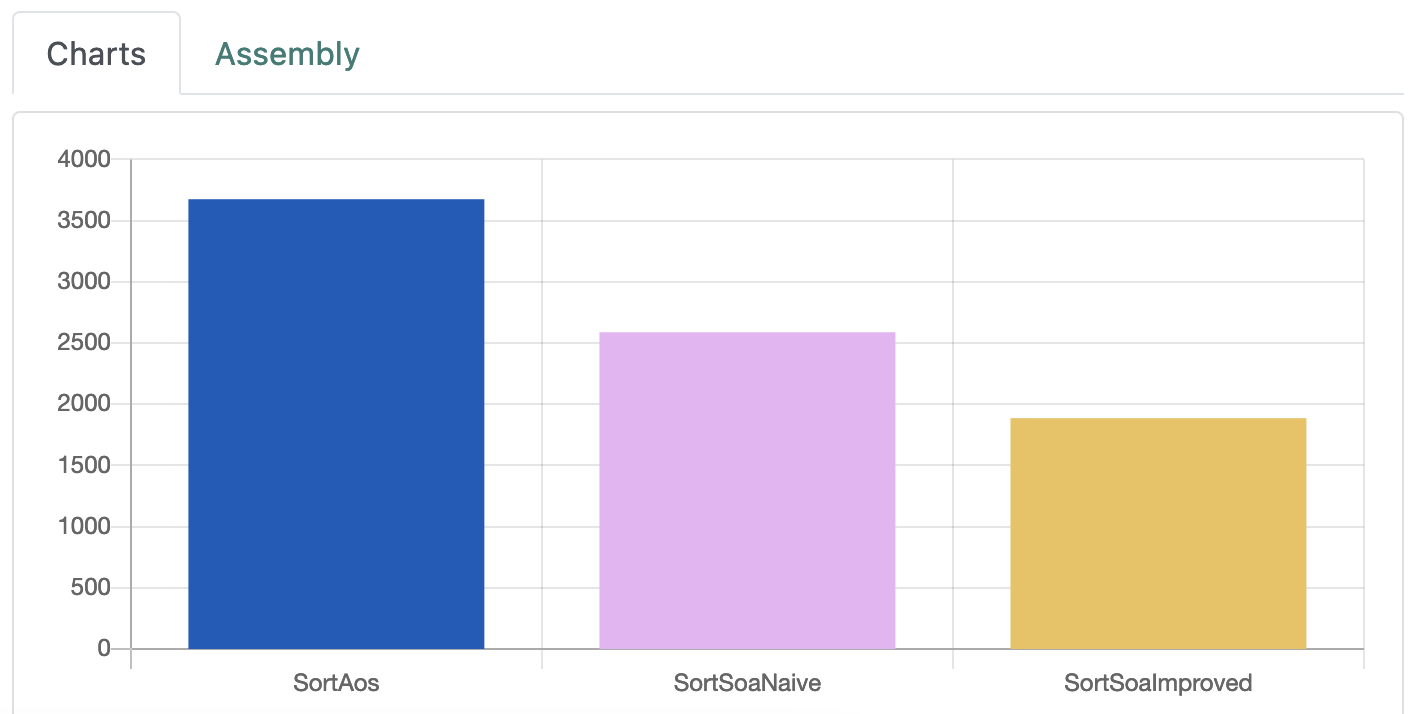
indirect sorting

There is also a Compiler Explorer (Godbolt) link here demonstrating the example from the article.

Further Reading

Please go read the awesome series by Raymond Chen on the Old New Thing blog about applying a permutation to a vector (and much more…).